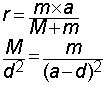Kirjankannen tarina

 

Kirja Orivesi ennen, VÄRIKUVIN. Kun kirja alkaa kannesta, niin eikös silloin ole loogista aloittaa kirjan tekeminen siitä? En tiedä muista kirjailijoista, mutta näin minä tein. Kirjan kannen pitäisi kertoa jotenkin kirjan sisällöstä. Minä olen tässä asiassa konkretian kannattaja, joten kannen kuvassa olisi näyttävä kirjan nimen kaikki kolme sanaa. Orivesi, ennen ja värikuvin. 

Kuvassa taustalla näkyvä Auvisen talo, nykyinen Taitokeskus, sijoittaa kuvan maantieteellisesti myös muille kuin paikkakuntalaisille tunnistettavasti Orivedelle – tai ainakin Mämmilään. Ylioppilaiden asut paljastavat, että kuva ei ole ihan viime vuosilta. Samoin oikealla oleva pyöräliike kertoo minun sukupolveni orivesiläisille kuvan olevan 50-luvulta. Tämä kirkonkylän vanhin asuttu rakennus, Kajaanipori, paloi vuonna 1959. Värillisyys näkyy tietysti siinä, että kansikuva on värillinen.

Näin ollen kuva tuntuu täyttävän nämä siltä vaaditut reunaehdot. Kerron tässä tarkemmin, miten kuva sai lopullisen muotonsa.

Kirja on B5-pystyformaattia. Koska halusin koko kannen kokoisen kansikuvan, senkin piti olla pystyformaattia. Ongelmaksi muodostui se, että käytössäni olleet kuvat olivat melkein kaikki joko neliön muotoisia tai vaakakuvia. Pystykuvissa ei ollut yhtään kansikuvaksi sopivaa. Uuttakaan ei voinut ottaa, kun ideana oli nimenomaan vanhat valokuvat väritettyinä. 

Tämä sittemmin valituksi tullut Esko Paavolan ottama kuva vuoden 1954 ylioppilaista marssimassa kohti kirkkoa viehätti minua jo alusta alkaen. Formaatti vain oli väärä, kuva on itse asiassa lievästi vaakakuva.

Valokuvan mittasuhteita voidaan muuttaa hieman ilman että sitä huomaa, jos ei ole vertailukohtaa. Tässä olen muuttanut kuvan neliöksi, mutta sehän on vielä kaukana halutusta formaatista.

Esko Paavolan arkistosta löytyi noin kymmenen vuotta nuorempi, samasta kohtaa Kanta-Hämeen liikkeen rappusilta otettu valokuva partiolaisista marssilla niin ikään kirkkoon. Kirkko tosin oli poltetun jälkeen uusi, kuten myös Kajaaniporin paikalle noussut kammottavan näköinen hökötys. Tästä muuten aika huonolaatuisesta kuvasta sain kuitenkin jatkettua vanhassa kuvassa torsoksi jäänyttä Kivilinnaa, kirkonkylän vanhinta kivitaloa. 

 Harppaan tässä muutaman välivaiheen. Jatkoin kuvaa alareunasta kopioimalla sinne lisää maantietä ja yläreunasta luomalla kuvaan kokonaan uuden taivaan. Sähköpylvästä piti myös rakennella ihan muista kuvista, koska sekin meni alkuperäisessä kuvassa poikki kuvan yläreunassa. Lopulta väritin kuvan ja lähetin sen ystävälleni Matti J. Kalevalle, joka oli luvannut auttaa minua kirjan visuaalisen ilmeen suunnittelussa. Vastaus tulikin aika pian. 

"Tuo kansiluonnos kertoo kyllä selkeästi mistä on kysymys, mutta kyllä siinä on tuollaisena sateenkaarena vähän liian halpa vivahde. Minusta tällainen kulttuurihistoriallisesti arvokas juttu ansaitsisi kannen, joka on jollain tavalla ”juhlallinen” tekstityypiltäänkin ja sen väritykseltä.

Kuva-aihe kanteen on mielestäni oikealla tavalla juhlallinen eikä silti liian vanhan postikorttimaiseman tapainen. Tosin juuri se ”neutraalimpi” maisema saattaa olla kaupallisesti myös pohdittavissa oleva vaihtoehto muutenkin vanhanaikaisen henkisellä kokonaissommittelulla. Sellaisena se saattaisi ehkä kiinnostaa enemmän turistia tai lahjateosta miettivää. Ostajia kun on monenlaisia, on varmasti niitäkin, joita juuri tämän kaltainen lehtikuvitusmainen aihe houkuttaa. Kannen kuvituksen hengen on luonnollisesti kuvastettava kirjan sisältöä tiivistettynä, joten tämä valitsemasi ratkaisu lienee erittäin hyvin perusteltavissa silloin, jos kuvitus painottuu nimenomaan tilannekuviin ja lehtiin aikanaan tarkoitettuun aineistoon."

Näiden kommenttien jälkeen päädyin aika pian lopulliseen kannen ulkoasuun. Sähköpylväs oli vielä katkaistava, koska se olisi muuten jäänyt häiritsevästi tekstin taakse. 

Ihan tällä kansikuva ei ollut vielä valmis. Kun kirjassa on kovat kannet, kansipaperia taitetaan reunan ylitse 17 mm. Se pitää ottaa huomioon kuvan lopullisissa mitoissa. Minun piti vielä jatkaa taivasta ylöspäin ja maantietä alaspäin sekä ottaa huomioon se, että myös kuvan oikeaa reunaa kääntyy kannen sisäpuolelle mainitut 17 mm. Mielelläni olisin jättänyt myös Kajaaniporin päätyikkunat näkyviin, mutta kaikkea haluamaansa ei aina voi saada.

Photoshopissa rakentamani kansipaperi oli tällainen. Olen merkinnyt tähän kuvaan punaisella leikkuuvarat ja selän osuuden. Edessä askeltavan tytön jalka ei saanut tulla liian lähelle alareunaa. Siksi maantietä on "rakennettu" kuvassa varmaan metrin verran.

Kansikuvassa on yksityiskohtia, jotka eivät painetussa kuvassa erotu kovin hyvin, mutta näkyvät tässä osasuurennoksessa. Polkupyörillä ajavilla tytöillä on molemmilla käsissään suklaapäällysteiset jäätelöpuikot. Siis entiset Eskimo- nykyiset Pingviini-puikot. Maantieteellisestihän tämä tarkoittaa siirtymistä pohjoiselta pallonpuoliskolta eteläiselle. 

Jäätelöä ei tähän aikaan myyty kaupoissa, vaan kioskeissa tai myyntikärryistä, joissa jäätelöt pidettiin kylminä hiilidioksidijään avulla. Käytännössä auto toi joka päivä Tampereelta Pyynikin tehtailta hiilidioksidijäätä Orivedelle jäätelönmyyjille. Nämä tytöt ovat ostaneet omat jätskinsä Auvisen vieressä olleesta kioskista.

Kuvassa keskellä on sittemmin mm. Mäntässä apteekkarina toiminut Tapio Peltonen ja hänen takanaan tämän kirjan ilmestymisen aikoihin kuollut lääketieteen professori Simo Tarpila.

Maailmankatu

 

Erkki Salomaa: Sarajevo, Bosnia-Herzegovina, 2012

Laterna Magicassa oli – ja meni – mielenkiintoinen näyttely Erkki Salomaa: Maailmankatu. Ei tullut käytyä monesta muustakin syystä kuin koronan pelosta. Tosin tappio ei ollut korvaamaton, koska sain lahjaksi kuvista tehdyn opuksen. Itse asiassa katselen valokuvia paljon mieluummin kotona valokuvakirjasta tai netistä kuin patsastelen valokuvanäyttelyssä. Kotona kuviin voi aina palata ja katsoa yhtä kuvaa sohvalla maaten niin pitkään kuin huvittaa. Näyttelyissä olin pyrkinyt käymään vain silloin, kun tekijä on ollut itse paikalla kertomassa kuvistaan. 

Maailmankatu on kaiken puolin pätevä katukuvauskirja. Sen lisäksi siinä on Hanna Weseliuksen hieno esipuhe. Suomeksi edelliset virkkeet tarkoittava sitä, että Salomaan käsitys katukuvauksesta ja  Weseliuksen valokuvauksesta, erityisesti katukuvauksesta on nähdyn ja luetun perusteella samat kuin minulla.  Siitä huolimatta vahva ostosuositus valokuvauksen harrastajille.

Erkki Salomaa: Funchal, 2015

Katukuvauksen suurimpia haasteita katsojaa ajatellen on se, että katsojalta puuttuu kuvan ottamistilanteeseen liittyvä tunnekokemus. Usein vielä paikat ja henkilöt ovat katsojalle täysin vieraita. Kosketuspintaa kuvaan on monesti varsin niukasti. Kaikki on revittävä irti itse kuvasta ja lähes pelkästään siitä. 

Muistan vieläkin hyvin katkerana muistona omilta valokuvauksen opiskeluajoiltani arvioijan kommentin, kun kerroin innoissani kuvan ottamiseen liittyneitä tunnelmia. Se kuului kaikessa lakoonisuudessaan: "Miten se näkyy kuvassa?". Sittemmin olen käyttänyt sitä useaankin kertaan, kun kuvaajat ovat kysyneet minulta arvioita kuvistaan pitkän ja vuolaan johdannon kera. Keskustelu on yleensä päättynyt siihen. 

Todettakoon tässä nyt vielä varmuuden vuoksi, että Erkki Salomaan kuvista välittyy ainakin minulle kuvissa vallitseva tunnelma. Niitä katsellessaan ei tunne myötähäpeää kuvaajaa kohtaan. Ne täyttävät hyvin katukuvauksen yhden keskeisen kriteerin, ratkaisevan hetken. 

Niin hienoja kuin Erkki Salomaan kuvat ovatkin, vähän kylmäksi ne jättivät minut. Pohdiskelin, miksi näin. Keittiöpsykologina tulin siihen tulokseen, että niistä puuttuu tuo aikaisemmin mainitsemani kosketuspinta minun suhteeni. En tunne kuvaajaa, en tunne kuvattavia, en tunne kuvauskohteita. Vertailuna mieleeni nousee äitini jo 50-luvulla New Yorkissa ottamat katukuvat. Äitini ei juuri kuvannut, mutta hänellä oli kyllä taiteellista silmää. Isäni oli ladannut hänelle kameraan rullan filmiä ja laittanut valotusarvot päivänvalon mukaan. Niillä piti pärjätä. 

Äitini harjoittelee kuvaamista ennen matkaansa.

Äitini ottama kuva New Yorkin kadulta. 

Eihän tämä mikään valokuvan historiaan jäävä katakuva ole, mutta minulle se antaa suuremman tunne-elämyksen kuin mikään Erkki Salomaan  objektiivisesti ottaen paljon vaikuttavampi valokuva. Vaikka fyysikkona tuppaan vaitimaan asioilta yhteismitallisuutta, emootio ei ole sitä millään tapaa. Pikemminkin päinvastoin.

Barysentri

Kuvakaappaus HS:n artikkelista

Lehtijutussa otsikon tarkoitus ei ole aina kertoa artikkelin keskeisestä sisällöstä, vaan houkutella lukijaa tarttumaan siihen. Tietämättä tämän taustoista sen enempää, omakohtainen kokemus on sellainen, että otsikko on usein eri henkilön laatima kuin itse artikkeli.

Hesarissa 7.7.2020 ollut artikkeli aurinkokunnan barysentrin eli massakeskipisteen (mkp) tarkasta määrittämisestä herätti vilkasta polemiikkia vanhojen fysiikan opettajien keskustelupalstalla. Juttu siis herätti kiinnostusta, mikä lienee hyvän lehtijutun tai ainakin aiheenvalinnan tarkoituskin. Artikkeli ei ollut toimituksen omaa tuotantoa, vaan pääosin käännetty alan julkaisuista. Ainakin tämä näyttää olleen yhtenä lähteenä, sen verran yhtenäisyyttä on sen ja Hesarin tekstien välillä

Itse julkaisu löytyy täältä. On selvää, että tiedetoimittaja, jolla on journalistinen, mutta ei fyysikon tai tähtitieteilijän koulutus takanaan, ei pysty oikein hyödyntämään alkuperäistä lähdettä. Ei ainakaan kaikilta osin. 

Valitettavasti toisen käden lähteissä olevat virheet ja epämääräisyydet tuppaavat siirtymään, kuten tässäkin on käynyt. Otan yhden esimerkiksi.

Ote yllä olevassa lehdessä

“Therefore, the precise gravitational centre (or barycentre) of the Solar System is not smack-bang in the middle of the Sun, but somewhere closer to its surface, just outside it.” 

Sama Hesarissa

"Aurinkokunnan tarkka painovoimien keskipiste ei ole lähellä valtavan Auringon ydintä. Sen paikka on juuri ja juuri Auringon pinnan ulkopuolelle."

Painovoimien keskipiste ei ole mielekäs fysikaalinen käsite. Homogeenisessa painovoimakentässä, kuten maapallon pinnalla olevien kappaleiden massakeskipiste ja painopiste ovat sama asia, mutta aurinkokunnassa tilanne on toinen. Jonkinlaisena ”painovoimien keskipisteenä” voisi pitää paikkaa, jossa aurinkokunnan kappaleiden, Auringon, planeettojen ja muun roinan painovoimien summa tässä pisteessä olevaan kappaleeseen on nolla. 

Joka tapauksella "painovoimien keskipiste" on eri asia kuin massakeskipiste.  Esimerkiksi Maan ja Kuun massakeskipiste, joka kiitos amerikkalaisten Kuuhun viemän etäisyysmittauspeilin tunnetaan hyvin tarkasti, on Maan sisällä.”Painovoimien keskipiste” sen sijaan on lähellä Kuuta, noin 350 000 km:n päässä Maan keskipisteestä. Todettakoon sivuhuomautuksena, että se on eri asia kuin Lagrangen pisteet , joilla on merkitystä mm. sellaisten satelliittien suhteen, joiden on tarkoitus pysyä paikoillaan avaruudessa.

Kaavakuva Maan ja Kuun barisentristä r ja "painovoimien keskipisteestä d, kumpikin mitattuna maapallon keskipisteestä. Maan ja Kuun keskipisteiden etäisyys on a. M ja m ovat taivaankappaleiden kappaleiden massat. r ja d ovat laskettavissa seuraavista yksinkertaisista yhtälöistä. Jätän laskemisen lukijan iloksi.

Aurinkokunnan massakeskipisteen paikka Aurinkoon nähden vaihtelee. Se on joskus lähellä Auringon keskipistettä, mutta välillä yli Auringon säteen päässä Auringon kehän ulkopuolella. Kuvassa massakeskipisteen rata Auringon suhteen noin 50 vuoden ajalta. ”Sen paikka on juuri ja juuri Auringon pinnan ulkopuolella” olisi vaatinut yhden tarkentavan sanan lisää, jotta lause olisi ollut paremmin ymmärrettävä tässä kontekstissa. "Sen keskimääräinen paikka on juuri ja juuri Auringon pinnan ulkopuolella."

Se, että aurinkokunnan mkp ja Auringon keskipiste poikkeavat toisistaan ja niiden välinen etäisyys vaihtelee, ei ole uutinen. Se on ollut tunnettu fakta jo vuosisatojen ajan. Kadunmies tulee tuskin koskaan pohtineeksi tätä seikkaa. Se kun ei tunnu arkisissa askareissa millään tavalla. Miksi sitten hurrata tulokselle, jonka mukaan aurinkokunnan massakeskipiste olisi saatu laskennallisesti selville 100 m:n tarkkuudella?

Syy on se, että monet astronomiset mittaukset pitää kiinnittää inertiaalikoordinaatistoon, jossa kappaleella on kiihtyvyyttä vain, jos siihen kohdistuu nettovoimia. Inertiaalikoordinaatisto on joko paikoillaan tai liikkuu tasaisella nopeudella. Auringon keskipisteeseen kiinnitetty koordinaatisto ei toteuta tätä ehtoa, mutta Aurinkokunnan massakeskipisteeseen sidottu koordinaatisto toteuttaa.  

Painovoima-aaltojen pitäisi teorian mukaan vaikuttaa pulsarien lähettämien pulssien havaittuun taajuuteen. Havaituilta taajuuseroilta putoaa tietyllä tavalla pohja pois, ellei niitä ole mitattu inertiakoordinaatistossa. Siksi aurinkokunnan mkp:n keskipisteen tarkan sijainnin tietäminen on tärkeää. Vasta sen koordinaatiston suhteen tehdyt mittaukset kertovat todelliset erot pulsarien taajuuksien poikkeamissa. Mitä tarkemmin tämä piste pystytään laskemaan, sitä tarkemmin pystytään sen avulla mittaamaan aikaan ja paikkaan liittyviä astronomisia suureita.  Ylläoleva kaavakuva antaa siinä mielessä väärän mielikuvan tilanteesta, että siinä on kuvattu Aurinko paikallaan olevana kappaleena ja massakeskipisten liikkuu sen suhteen. Inertiaalikoordinaatistossa mkp on paikoillaan ja aurinkokunnan kappaleet Aurinko itse mukaanlukien liikkuvat mkp:n suhteen.

Kyse on nimenomaan mkp:n paikan laskemisesta. Aurinkokunnan mkp inertiaalikoordinaatiston keskipisteenä on laskennallinen abstraktio, sen paikkaa ei voi mitata. Siksi tässä kohtaa Hesarin yksi artikkelin  lause iskeekin fyysikon silmin tekstiä luettaessa pahasti näpeille: ”AURINKOKUNNAN keskipisteen mittauksessa”. 

Ainakin minun kouluaikana ainekirjoituksen synneistä pahimpiin kuului tautologia. Tautologian saastuttamasta aineesta oli turha odottaa kiitettävää arvosanaa. Ehkä juuri siksi toimittajat pyrkivät välttämään tautologiaa kuin ruttoa. Väliin seurauksena vain voi olla, että käytetään synonyymeina ilmaisuja, jotka eivät olekaan sitä. Kuten laskeminen ja mittaaminen.

Tutkimusraportin alla olevassa tiivistelmässä itse asiassa on kerrottu kaikki oleelliset seikat siitä, mistä tässä on oikein kysymys. Miten näistä faktoista kasaa suurta yleisöä kiinnostavan tiedejutun, on toinen asia. Kun jo pelkästään sen perusasian tietäminen, että pulssien epäsäännöllisyyden tarkka mittaaminen vaatii inertiaalikoordinaatiston, tuskin kuuluu kovin monen Hesarin ”maallikkolukijan” yleissivistykseen. 

"Abstract

The regularity of pulsar emissions becomes apparent once we reference the pulses' times of arrivals to the inertial rest frame of the solar system. It follows that errors in the determination of Earth's position with respect to the solar system barycenter can appear as a time-correlated bias in pulsar-timing residual time series, affecting the searches for low-frequency gravitational waves performed with pulsar-timing arrays. Indeed, recent array data sets yield different gravitational-wave background upper limits and detection statistics when analyzed with different solar system ephemerides (taivaankappaleiden liikkeiden taulukko). Crucially, the ephemerides do not generally provide usable error representations."

Artikkelin varsinainen pihvi on siis siinä, että aurinkokunnan massakeskipiste on selvitetty laskemalla tilastomatemaattisin keinoin 100 metrin tarkkuudella taivaankappaleiden taulukoitujen liikkeiden avulla. Onko näin suureen tarkkuuteen todella päästy, se selviää vasta, kun tämän inertiakoordinaatiston avulla saadaan mittaustuloksia pulsareiden taajuuksien epäsäännöllisyyksistä. Niitä odoteltaessa tarkkuus on vain hypoteesi.

Tämän postauksen tarkoitus ei ole mitenkään irvailla tai besserwisseröidä Hesarin artikkelin suhteen, vaan esimerkin valossa tuoda esille, miten vaikeaa tehdä tiedejuttua, jossa toimittaja joutuu tasapainoilemaan syvällisen aiheen monimutkaisten faktojen, lukijoiden mielenkiinnon herättämisen ja tekstin yleistajuttavuuden kanssa. Aika usein vielä oman ymmärtämisensä äärirajoilla, jommalla kummalla puolella.  

Sekä Helsingin Sanomat että saman konsernin Tiede-lehti ovat minusta ansioituneita myös minun edustamani "kovien luonnontieteiden" kansantajuisessa uutisoinnissa.  Etenkin kun niiden herättämä yleinen mielenkiinto on sittenkin yleensä aika vähäistä. Mikäli jotain voi päätellä tämänkin artikkelin Hesarin sivuilla kirvoittaman keskustelun kommenttien määrästä ja keskustelun tasosta. Kiinnostus juuri tätä artikkelia kohtaan oli fysiikan opettajien keskutelupalstalla paljon suurempi. Edelleen mikäli jotain voi päätellä kommenttien määrästä ja keskustelun tasosta.

Itsekin artikkelia lukiessani tuskin olisin kiinnittänyt mitään huomiota näihin mainitsemiini asioihin, ellei entinen fysiikan opettajani professori Kaarle Kurki-Suonio olisi ottanut niitä esille kyseisellä fysiikan opettajien keskustelupalstalla. Kaarlen kommentit saivat minut kiinnostumaan aiheesta, joten siinä mielessä artikkeli puutteineen (tai ehkä juuri siksi) innosti minua ottamaan selvää jutun takana olevasta fysiikasta. Voiko tiedeartikkelilta lukijan suhteen enempää vaatia? Ei ainakaan minun kohdallani.