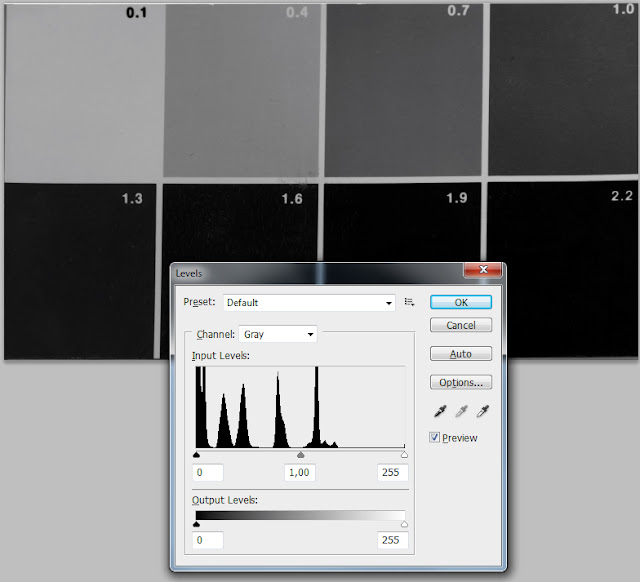
Toinen kuva on valotettu siten, että histogrammin oikea pää juuri ja juuri koskettaa oikeaa reunaa, eli ETTR. Toinen on valotettu tästä kaksi aukkoarvoa ali, mikä menee jo ohitse ETTL:n, mutta näin saan ilmiön paremmin havainnollistettua.
Jos oletetaan että alkuperäinen kuva olisikin ollut negatiivi, jolloin sen negatiivi olisi tietysti positiivi. Marssijärjestys kääntyy. Nyt ETTL-periaatteella (jopa niin vasemmalle mennen, että hirvittäisi entistä Maalaisliittoakin) kuvasta saisi tummasta päästä sävykkäämmän positiivin. Eri sävyjen määrä ei tässä käännöksessä tietenkään kasva, mutta yläpään kapeampi sävyala ja vähempi sävyjen määrä ei haittaa, koska näköaisti ihmisaisti ei tee suurtakaan eroa oheisten kuvien yläpään sävyeroille. Se johtuu näköaistin logartmisuudesta.
Lopuksi vielä pieni matematiikkapläjäys. Jos haluaisi tietää, miten paljon vaikka densiteettiarvolla 0,7 varustettu pinta heijastaa valoa, niin seuraava laskutoimitus kertoo sen.
Vastaus on siis 20 %. Se on aika lähellä harmaakorteissa käytettyä arvoa 18 %, jonka heijastavan pinnan densiteetti taas on 0,74.






5 kommenttia:
Must ei ois ikinä tullut valokuvaajaa jos hommat olis pitänyt hoitaa aina logaritmin neliöjuuren cosinilla :-) Cosina taas oli kamera.
Sinusta ei olisi ikinä tullut valokuvaajaa, jos joku ei olisi hoitanut näitä "logaritmin neliöjuuren cosineita" sinun puolestasi. Ilman heitä olisit korkeintaan piirrellyt kepillä kuvia rantahiekkaan.
Puusa-Suvanto: 0-6
Ei tässä mistään ottelusta ole kysymys, ei ainakaan minun osaltani. Valokuvauksella on monia ulottuvuuksia. Jotkut ovat kiinnostuneita enemmän laitteista kuin valokuvista, jollekin kuvausretki on vähän niin kuin kalastusretki toisille. Tärkeintä ei ole saalis vaan retkellä olo. Minä olen kiinnostunut, en ainoastaan mutta myös, valokuvauksen matematiikasta ja fysiikasta. Ei kai siinäkään mitään moitittavaa ole. Näitä juttuja esittelen sitten täällä blogissani muille näistä asioista kiinnostuneille. Se on niin yksinkertaista.
Nono eipäs olla niin ärtsyjä :-) kepillä voisi olla kiva piirrellä valokuvaamisen sijaan.
Tässä oli itseeni kohdistuvaa sarkasmia.
-
Mutta tuota Puusa - Suvanto 0-6 en ymmärrä ollenkaan, laskin vain leikkiä täydellisestä matemaattisesta kyvyttömyydestäni. Ilmeisesti sekin oli liikaa fotarille.
Mun kilpailut on kilpailtu.
Lähetä kommentti