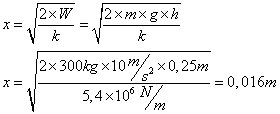Norsu Heurekan vaijeripyörässä

Jorma Eton tunnetun runon mukaan:

Suomalainen on sellainen, joka vastaa kun ei kysytä,

kysyy kun ei vastata, ei vastaa kun kysytään,

sellainen, joka eksyy tieltä, huutaa rannalla...

Muut tuntomerkit kyllä sopivat, mutta minä vastaan joskus myös silloin, kun kysytään. Kuten nyt alla olevan kirjeenvaihdon perusteella.

"Moi, tällaista on kysytty:

Vaijerin paksuus ja pituus ja mikä on vaijerin jännite tai siis millä voimalla vaijerinpäitä vedetään tai siis JOS päissä olisi tukipisteet, joiden yli vaijerinpäät kulkisivat ja veto olisikin hoidettu vaijerissa roikkuvilla painoilla, niin PALJONKO olisi painoa päissä?

Heko"

Tätä nyt ei kysytty minulta vaan Jussi Savalta, mutta kun olin hänen vastauksensa postituslistalla, niin voinen vastata myös tähän.

"Terve Heko

Vaijeri on 20mm paksu. Ajomatka on n. 21 metriä, ja vaijerin kokonaispituus on n. 30m. Tuohon vetolujuuteen minulla ei ole suoraa vastausta. Kuormia on laskettu niin, että vaijerin painumaksi tulee 23cm pelkän polkupyörän painolla. Kun polkupyörällä ajaa 130 kiloinen henkilö, painumaksi tulee 35cm. Tuossa maksimipainoisen ajajan tapauksessa vaijerivoima kasvaa arvoon 50kN.

En usko, että on mahdollista käyttää tuota painuman muutosta sellaisenaan hyväksi, mutta painuma siis kasvaa ajajan myötä 1.5 kertaiseksi verrattuna pelkän pyörän aiheuttamaan painumaan. Jos tuolla kertoimella kuitenkin miettii vaijerivoimaa ilman 130kg ajajan vaikutusta, vaijerivoima olisi n. 33kN. Tuolloin vaijerin päällä on siis pelkkä pyörä, joka painaa n. 150kg. En tiedä, mikä on vaijerivoima ilman vaijerin päällä olevaa kuormaa.

Nuo edelliset kN:t muutettuna kiloiksi olisivat n. 5000 ja 3300 kiloa. Vaijerin murtokuormaksi on ilmoitettu 342kN, eli n. 34000 kiloa. Seinäkiinnikkeet kestävät n. 300 kilonewtonia, eli n. 30000 kiloa.

Osaisiko Timo spekuloida tarkemmin, voiko yllä olevilla tiedoilla laskea vaijeripyörän vaijerin vetolujuuden kohtuullisella vaivalla?

yst. Jussi"


Edellisessä elämässäni lukion fysiikan opettajana tuli laskettua kerran jos toisenkin seinälle ripustetun taulun lankaan kohdistavaa jännitystä. Sitä kuten ei sähköopinkaan laskuja opi laskemaan Korkeajännityssarjaa lukemalla. Kyllä siihen tarvitaan ihan rehellisiä fysiikan opintoja - tosin lukiosellaiset riittävät tähän.

Vaijeriin kohdistuvan jännityksen laskeminen perustuu oheiseen koulufysiikasta tuttuun menetelmään. Vaijerin jännityksen aiheuttamat voimat voidaan jakaa kahteen komponenttiin. Vaakasuorat komponentit kumoavat toisensa ja pystysuorien komponenttien summa on yhtä suuri kuin vaijerin kannattaman esineen paino.

M = T_1y + T_2y

Pyöräilijän ollessa keskellä vaijeria vaijerin pyörää ylöspäin vetävät jännitykset ovat molemmilla puolilla yhtä suuret, eli silloin

T = T₁ = T₂

T = M/2*(T_1x/T_1y)

Silloin kun vaijerilla ei ole pyörää, sen jännitys tulee vaiajerin omasta painosta ja siitä, kuinka tiukkaan vaijeri on kiristetty seinään. Oman painonsa johdosta vaijeri asettuu ns. ketjukäyrän muotoon, myös silloin kuin se on kiristetty. Kiristämisen johdosta vain suhteellisesti pienempi osa koko ketjukäyrästä on vaijerin muodossa.

Ketjukäyrä. Ilman ulkoista kuormaa olevassa Heurekan pyörävaijerissa on korkeintaan kolmen alimmaisen lenkin verran ketjukäyrän muotoa.

Vaijerin oman painon aiheuttama jännitys ei ole vakio, vaan kasvaa lähestyttäessä vaijerin lähtölavalla olevia tukipisteitä. Tämä on varsin ymmärrettävää, kasvaahan vaijerin kunkin kohdan kannateltava paino mukaa, mitä enemmän vaijerin massaa ko. kohdalla on kannateltavanaan. Vaijerin jännitys tässä tapauksessa on suurin juuri ennen tukipistettä. Onkin luontevaa laskea tämä jännityksen maksimiarvo, onhan se vaijerin kestävyyden kannalta oleellisin. 

Jännityksen laskemiseen tarvittavan vaijerin kaltevuuskulman saa selville vatupassilla (pituus 60 cm), mittanauhalla ja trigonometrialla. Itse asiassa kulmaakaan ei tarvitse laskea, kun laskuissa tarvittavat sinit ja tangentit ovat pienillä kulmilla suunnilleen yhtä suuret. Siitä koituva heitto häviää muiden mittavirheiden sekaan.

Mittasin vatupassilla, kuinka paljon vaijeri poikkeaa vaakasuorasta suunnasta ilman pyörän ja pyöräilijän painoa juuri ennen tukipistettä.

Vaijerin kaltevuus saadaan selville mittaamalla, paljonko se oli pudonnut vaakasuorasta vatupassin mittaisella matkalla ( 60 cm). Käytännössä tämä  mittaus oli helpointa tehdä niin, että justeerasin etusormi vaijeriin tukien vatupassin vaateriin ja mittasin sitten etusormen ja vatupassin reunan välisen etäisyyden. Tulos oli 6 mm. Tässä lasketaan suuruusluokka-arvoja, eikä 5 merkitsevän numeron tarkkuudella.

 Vaijerin kierrerakenne mahdollistaa vaijerin pituuden kasvamisen jännityksen lisääntyessä ilman, että on pelkoa vaijerin katkeamisesta. Heurekan vaijeri venyy noin 2*2,5 mm = 5 mm, kun 80 kiloinen pyöräilijä ajaa sen päällä. Tulosta epäilevät voivat tarkistaa asian herra Pythagorakselta.

Vaijeri on 20 mm paksua terästä ja  tukipisteiden väli on 25 m pitkä. Kun teräksen tiheys on noin 8000 kg/m^3, niin peruskoulutason laskulla  saadaan sylinterin muotoisen vaijerin pätkän painoksi.

Vaijerin jännitykseksi ilman kuormaa tulisi silloin

Olen käyttänyt tässä kaikkia puritaaneja fyysikkoja hirvittäen kilogrammoja painon ja jopa voiman yksikkönä. Tämä tulos tarkoittaa sitä, että samaan jännitykseen päästäisiin laittamalla vaijerin toiseen päähän roikkumaan 3000 kg paino. Painoahan ei tarvitse olla kuin toisessa päässä, toinen pää voisi olla pultattu seinään. Toki voidaanhan painot laittaa molempiinkin päihin, jos vaikka syystä tai toisesta ei haluta tehdä reikää seinään.

Kun vaijerin päälle tulee 150 kg painava pyörä ja  80 kg painava pyöräilijä, niin vaijerin oma paino ei vaikuta enää niin paljon. Mittaamalla taas vaijerin kallistuman saadaan suuruusluokka-arvio vaijerin jännitykselle pyöräilijän ollessa puolessa välissä matkaansa. Vatupassin pään ja vaijerin välinen etäisyys on nyt 20 mm.

Satunnaisessa koetilanteessa ei tämän painavampaa polkijaa sattunut paikalle. 50 kg pitäisi saada vielä painoa lisää, jotta voitaisiin testata tilanne tuon kuvitellun maksimikuorman tapauksessa.Tilannetta se ei tulisi siinä mielessä muuttamaan, että vaijerin jännitys on tuhdimmankin polkijan alla moninkertaisesti alle riskirajojen. Jos seinäkiinnitys haluttaisiin korvata vaijerin päässä roikkuvalla painolla, niin 5000 kg painava norsu voisi olla aika passeli.

Vaijerin seinäkiinnitys herättää ainakin minussa luottamusta sen kestävyyteen.Tämän avulla siis vaijeri pysyy seinässä kiinni ja ruuvisyateemillä se kiristetään haluttuun jännitykseen.

Mittausteni perusteella saamani tulokset on siis hyvin linjassa Jussin esittämän kanssa. Vaijerin ja seinäkiinnikkeiden  kestävyydestä en osaa sanoa mitään, ne ovat insinöörien asioita. Kun ne ovat kestäneet jo parikymmentä vuotta, niin eiköhän noihin laskelmiin voitane luottaa.

Minulta on joku kysynyt, että voisiko vaijerin saada katkeamaan spöijaamalla eli keinuttamalla pyörää ylös ja alas keskellä vaijeria. Fysikaalisesti tilanne muuttuu paljon haastavammaksi, koska systeemi ei ole enää staattinen vaan dynaaminen.  Jotta sille saataisiin jonkinlainen laskennallinen arvio, pitäisi tietää mm. vaijerin kimmo-ominaisuuksia. Turvakert oimet ovat niin suuret, että olen aika varma rakenteiden kestävyydestä. En kuitenkaan kehota kokeilemaan, pikemminkin kiellän. Jokainen auton renkaita itse vaihtanut tietää, miten pahastikin ruostuneet mutterit alkavat kiertyä auki, kun spöijaa koko painollaan vääntöavaimen varren päällä. Kohta sekin on taas edessä.

 Tiedekeskus Heurekan vaijeripyörän vaijeri vajoaa  keskikohdaltaan pyöräilijän alta suunnilleen pyörän säteen verran eli noin 25 cm. Tässä on lisätty vaijeri kuvasta, jossa kukaan ei ajanut vaijerilla.Vaijerin kireys on kompromissi. Tiukalle vedetty vaijeri vajoaa vain vähän raskaankin kuorman alla, mutta seinäkiinnikkeet ovat kovilla. Jos vaijerin jännitys on liian pieni, niin varsinkin pyöräilyn lopun ylämäki on ainakin pienemmille polkijoille ylivoimainen. Heurekan vaijerin kireys on aika passelin tuntuinen kompromissi.

Jälkikirjoitus

Kun minulta kysyttiin, että voiko edes antaa jonkinlaisia arvioita siitä vaijerin jännityksestä, jonka siihen voisi pyörää ylös ja alas heijaamalla saada, niin lupasin koettaa luoda asiasta jonkinlaisen matemaattisen mallin olettaen, että kierteinen vaijeri toimii tässä kuten jousi. Eri mieltä olevat saavat vapaasti esittää parempia malleja, "Väärin sammutettu" kommentteja en kaipaa.

  

Kaavassa F on kuorman jouseen vaikuttava voima jousen venymän ollessa x. W on jousen jännitystä vastaan tehty työ ja k on kullekin jouselle ominainen jousivakio. 

Aikaisempien tulosten perusteella saadaan, että 80-kiloisen pyöräilijän ollessa vaijerin keskikohdalla vaijerin jännitys kasvaa 1350 kiloa eli noin 13500 newtonia ja samanaikaisesti vaijeri venyy pyöräilijän molemmin puolin noin 2,5 mm. Näistä arvoista voidaan laskea k:n arvo.

Jos oletetaan, että pyöräilijä heijaa pyörää ylös ja alas siten, että pyörä putoaa alkuperäisestä tasapainoasemasta normaalin 25 cm matkan. Vaijeri joutuu nyt kovemmalle, koska siihen sitoutuu pyörän pudotessaan saama liike-energia. Samalla vaijerijousen pituus kasvaa.

Vaijeri venyisi siis tämän heijaamisen johdosta 1,6 cm puolikkaalta pituudeltaan eli 12,5 metrin matkalla. Pythagoraan lauseen avulla voidaan laskea, miten alas pyörä tällöin putoaisi ennen kuin vaijerin jännitys pysäyttäisin sen. 

Kun pyörä nousee vaijerijousen sinkauttamana ylös, niin seuraavalla kerralla se putoaa aina vain alemmaksi. Toisaalta langan venyessä sen jännitys lisääntyy ja jossain vaiheessa päästään tilanteeseen, jota alemmaksi pyörä ei enää vajoa. Kokeilemalla edellä oleviin lausekkeisiin eri putoamiskorkeuden a:n arvoja havaitaan, että tasapainotila saavutetaan noin 75 cm kohdalla. Sen alemmaksi pyörää ei heijaamalla juuri saa. Vaijeri venyy tällöin noin 2,8 cm vaijerin puolikkaan matkalla. Jousivoiman lausekkeesta voidaan nyt laskea vaijeriin tässä tilanteessa kohdistuva jännitys.

Tämä voima vastaa siis noin 15000 kg kuormaa. Seinäkiinnikkeille ja vaijerille on luvattu kaksinkertaiset murtolujuudet tähän verrattuna.

Ennen kuin ruvetaan vaatimaan paksumpaa vaijeria ja lujempia seinäkiinnityksiä (tai isompia norsuja kaksin kappalein), pari huomautusta. Laskelmat perustuvat yksinkertaistettuun matemaattiseen malliin, jonka tosin oletan antavan suuruusluokaltaan oikeita tuloksia. Toiseksi pyörän heijaaminen siten, että tämä maksimipoikkeama saavutetaan, vaatii jo melkoista rämäpäisyyttä. Niinä parina kertana, jolloin minä olen havainnut edes hieman siihen suutaan tapahtuvaa pelleilyä vaijeripyörällä, henkilökunta on puuttunut tilanteeseen viipymättä ja päättäväisesti. Heurekan kaltaisella instituutiolla ei ole varaa antaa kenenkään loukata itseään sen laitteissa, vaikka se kuinka olisi pelkästään kävijän omasta tyhmyydestä johtuvaa.

Arkipäivän suhteellisuusteoriaa

Einsteinin suhteellisuusteoriaa pidetään yhtenä mullistavimmista maailmankuvamme vallankumouksista. Suhteellisuusteorian mukaahan aika ei suinkaan virtaa absoluuttisella nopeudella eteenpäin, vaan on hyvinkin suhteellista riippuen mm. kelloon katsojan nopeudesta tai gravitaation voimakkuudesta.

Sinänsä ajatus ajan suhteellisuudesta on ylimainostettua nerokkuutta. Jokainen seniori-ikään ehtinyt ei ole voinut olla huomaamatta, kuinka aika kuluu aina vain nopeammin, mitä enemmän sitä on taakseen jättänyt.. ”Niin se aika rientää” lienee yhtä tavallinen toteamus meidän ikä-ihmisten kohdassa kuin vaikka ”On se ilmoja pidellyt”. Molemmat pitävät sisällään samanlaisen itsestään selvyyden. Jos maapallo ei pitelisi ilmoja, niin aika ahdistavaksi kävisi elämällä täällä. Kuten myös ajan kokonaan pysähtyessä, kuten kävi Raamatussa Jumalan pysäyttäessä Auringon keskelle taivasta (Joos. 10:12–13.).

Oulun yliopiston matematiikan emeritusprofessori Heikki Haahti on luonut matemaattisen kaavan sille, miten subjektiivisen eli tuntemuksellisen ajan muuttuminen riippuu iästä. Tutkimus julkaistiin Suomen fyysikkoseuran ja Suomen Matemaattisen yhdistyksen lehdessä Arkhimedes. Perusteellisten ja tiedeyhteisön kritiikin läpikäyneiden (luulisin ainakin) teoreettisten ja kokeellisten tutkimusten perusteella Haahti on tullut siihen tuloksen, että objektiivisen ajan  muutosnopeus dt suhteessa subjektiivisen ajan muutokseen dT riippuu lineaarisesti objektiivisesta iästä. Siis

dt/dT = at+b

Tutkimuksen kokeellisessa osassa professori Heikki Haahti on selvittänyt, että subjektiivinen ja objektiivinen ikä on yhtä isot 15-vuotiaana.  60-vuotiaan subjektiivinen aika rientää jo kaksi kertaa niin nopeasti kuin objektiivinen aika.

Näistä reunaehdoista voidaan ratkaista yllä oleva differentiaaliyhtälö.  Subjektiivinen aika objektiivisen ajan funktiona on

T(t) = 45*ln(t+30)/30)

Siis esimerkiksi minusta tuntuisi tämän perusteella, että vaikka olen elänyt jo 61-vuotiaaksi, niin subjektiivisesti se tuntuu 50 vuodelta. Aika monta päivää on tullut vaihdettua pois saamatta mitään tilalle. Sen sijaan pojantyttäreni Jessikan 7 objektiivista ikävuotta tuntuvat hänestä 9½ vuodelta. Ilmankos hän pitääkin itseään jo isona tyttönä.

Ikä ei suinkaan ainoa, joka saa ajan kulumisen tuntumaan erilaiselta. Väliin aika tuntuu matelevan etanan lailla, väliin taas saavan siivet selkäänsä. Minun nuoruuteni suuret kotimaiset iskelmätähdet Danny ja Johnny molemmat  filosohveerasit samasta teemasta. Näin Danny eli Ilkka Lipsanen laulussa "Kauan".

”Toisien kanssa kun sä tanssit,

Niin aina levy silloin soi kauan

Ulos kun iltaisin mä odotan sua,

Sä aina viivyt niin kauan

Vaan yhdessä kun ollaan,

Aika saa kuin siivet selkään,

Kaupunkimme kellojen

Mä edistävän pelkään

Miksi on niin

Mä nähdä sun, armahin

Jo heti aamulla aikaisin haluaisin,

Ja sun kauan kanssani kulkevan,

Kauan kellojen seisovan,

Kauan haluan jatkuvan niin

Kauan, kauan…”

Johnny eli porvarillisemmin Eljon Liebkind taas tuskaili laulussaan ”Tunti vain”, että

”Tunti vain!

Voi voi, kun viisarit käy vitkaan…”

Johnny oli laulun tekstin mukaan saanut jälki-istuntoa nykymittapuun mukaan aika vähäisestä asiasta, eli jättämättä koulussa vastaamatta opettajan kysymykseen. Mielessä oli silloin jotain muuta.

Oikeassa elämässä Eljonille kävi köpelömmin. Hän joutui virumaan 90-luvun puolessa välissä Israelissa 10 kuukautta tutkintovankeudessa rahanpesusta epäiltynä. Ehkä sellissä tuli tapailua uudistettuja laulun sanoja: ”Voi voi, kun maapallo pyörii radallaan vitkaan”.

Australialaisen lähellä Melbournea sijaitsevan Nonexistencen yliopiston psykologian laitoksen tutkija Dr. Nicholas Oswald Nathan Sence on luonut  matemaattisen mallin ajan subjektiivisesta kulumisesta riippuen siitä, onko kivaa ja mielenkiintoista vai  tylsää ja ikävää. Kaava laskee tunnin subjektiivisen pituuden minuuteissa objektiivisen ajan funktiona.

T(t) = 123,4/ln(1,52+0,216*M)

missä M on ns. mielenkiinto-kerroin, jolle annetaan arvoja välillä 0 – 10. M = 0 edustaa niin sanottua EVVK-tilaa, eli tylsintä tai epämiellyttävintä mahdollista olotilaa. Hammaslääkärin tulissa juurihoitoa saamassa tai pakkoruotsin tunti Pelkosenniemen yläasteella on antaa hyvän mielikuvan nollaa lähestyvästä M:n arvosta. M:n arvolla 10 taas vauhti on päällä, kuten vaikka ravintolan pikkutunneilla juuri ennen kuin paikka menee kiinni ja joku pitäis saada.  Neutraalia olotilaa, siis jonkinlaista ei kuulu hyvää eikä huonoa edustaa M = 5.

Muutamia subjektiivisen tunnin objektiivisia arvoja.

T(0) = 57,4/ln(1,52 + 0,216*0) = 137 min = 2 h 17 min.

T(5) = 57,4/ln(1,52 + 0,216*5) = 60 min

T(10) = 57,4/ln(1,52 + 0,216*10) = 44,0 min

Siis lohdutuksena niille, joista aika tuntuu välillä matavan kiusallisen hitaasti, niin ei tunti pahimmillaankaan tunnu kuin reilulta kahdelta tunnilta ja vartilta, vaikka olisi kuinka tylsää ja ikävää. Toisaalta oikein mukavassa seurassa tunti kestää mielessäkin sentään melkein kolme varttia. Kyllä siinä ajassa ehtii tehdä vaikka mitä. 

Ajan  subjektiivinen kuluminen mielenkiinnon funktiona

Analogista lisäketodellisuutta

Kuva: Jani Koivula

Poikkitieteilijä tutustumassa puolalaiseen lisäketodellisuuteen Varsovassa vanhan kaupungin liepeillä. Kuva ei liity aiheeseen millään muulla tavalla kuin siten, että se oli ainoa minusta reissussa otettu kuva. Valokuvaaja itse kun tuppaa jäämään aina kameran "väärälle" puolelle. 

Lech-olut ei  tiettävästi liity Lech Walesaan muutoin kuin siten, että lähteiden mukaan molemmat Lechit tulivat hyvin toimeen keskenään.

Osallistuin kesällä 2011 Varsovassa Copernicus tiedekeskuksessa järjestettyyn Euroopan tiedekeskusten yhteisön ECSITE:n vuotuiseen konferenssiin. Olin saanut matkaa varten Suomen Tiedetoimittajilta apurahan ja tarkoitukseni oli tutustua siihen, miten Copernicuksessa oli tehty eri tiedekeskuskohteille oheismateriaalia, sanallista valo- tai videokuvilla mahdollisesti terästettyinä. Tämä kun on ollut mielenkiintoni kohteena viimeisten kolmen vuoden ajan kahdessa suuressa EU:n rahoittamassa opetusmateriaalihankkeessa: Cosmoksessa ja Open Sciense Resourcessa.

Osuuteni näissä projekteissa on pääosin ohitse, mutta jälkihoitona teen pientä omaa tutkimustani siitä, mitä vaikutusta ja merkitystä niissä tekemälläni materiaalilla on tiedekeskus Heurekan toiminnassa. Tiedekeskus on niin kompakti kohde, että siellä on mahdollista kohtuullisilla kustannuksilla tutkia, miten työni tiedetoimittajana tai tietokirjailijana fysiikan popularisoijana otetaan vastaan. Lankeaako siemen hedelmälliseen maahan vai meneekö vesi hanhenselkää pitkin? Helmiä sioille vertausta en tässä yhteydessä käyttäisi, joku voisi ymmärtää sen väärin.

Konferenssien ohjelmat tehdään kuitenkin yleisen, ei yksityisen osanottajan mielenkiinnon perusteella. Minun kannaltani oikeastaan ainoa todella mielenkiintoisessa sessiossa käsiteltiin näyttelykohteiden tekstien ja itse näyttelykohteen välistä suhdetta. Sattumoisin tanskalainen tohtoriopiskelija Anne Kahr-Højland oli tutkinut suunnilleen samaa asiaa mistä minäkin olin kiinnostunut, eli näyttelykohteen fysikaalisen taustan selkeyttämistä oheismateriaalin avulla. Käyntikortit vaihdettiin ja olemme olleet enempi vähempi säännöllisessä sähköpostiyhteydessä kesän ja syksyn aikana. Henkilökohtaiset kontaktit ja niihin liittyvä verkostoituminen tuppaavat sittenkin olemaan konferenssien parasta antia. Muun tarjonnan mielenkiintoisuudesta riippumatta.

Toinen mielenkiinnon kohteeni tässä konferenssissa oli Augment Reality eli lisäketodellisuus. Sillä tarkoitetaan yleisesti ottaen esillä olevan asian tai ilmiön piilossa olevien seikkojen saattamista näkyville modernin teknologian keinoin reaaliajassa.. Esimerkiksi lentäjän kypärän visiiriin heijastettu tieto koneen tilasta keinohorisontteineen on tyypillinen lisäketodellisuus.  Opetuksessa lisäketodellisuus hakee koko ajan uusia sovelluksia. Minä olen törmännyt lisäketodellisuuteen mm. Science Center To Go hankkeessa. Siellä rakennetussa lisäketodellisuudessa voi esimerkiksi havaita kaasumolekyylien liikkeen muutokset lämpötilan muuttuessa.

Varsinaiseen lisäketodellisuuteen ei konferenssissa törmännyt. Sen sijaan minua kiehtoi kovasti tiedekeskuksessa ollut kaasujen lämpöliikettä suuressa mittakaavassa perinteisellä tavalla demonstroiva laite. Siitä kaasuatomeja markkeeraavat pingispallon pannaan kiivaaseen liikkeeseen voimakkaan puhalluksen avulla. Kun "kaasuastian" tilavuutta voidaan vielä säätää, niin laitteella voidaan havainnollistaa vielä tilavuuden ja kaasun paineen välistä riippuvuutta tavalla, joka varmasti jättää muistijäljen.

Tätä laitetta ei mitenkään voi pitää lisäketodellisuutena, sillä katsoja ei tunne mitään lämpötilan muutoksia. Kyseessä on siis simulaatio, mikä on eri asia kuin lisäketodellisuus. Siitä huolimatta en voinut olla vertailematta lisäketodellisuuden kaasuatomien liikettä ja tämän laitteen pallojen liikettä. Voidaanko niitä laittaa jotenkin paremmuusjärjestykseen?

Uskon, että ei. Lisäketodellisuudessa yhdistyvät kaksi asiaa reaaliajassa: lämpötila ja molekyylien erilainen liike. Pedagoginen punainen lanka on silloin yhtäläisyysmerkin polttomerkintä aivoihin näiden kahden asian välille. Tiedekeskuksen demossa, niin vaikuttava kuin se muuten onkin, täytyy katsojalla olla tieto kaasujen lämpöliikkeestä etukäteen tai se selitetään hänelle demon yhteydessä. Lämpimän tai kylmän tunnetta hänellä ei kohdetta katsottaessa ole.

Kehittelinkin tälle kohteelle innovaation. Vierailija voi työntää kätensä kahteen onkaloon., joista toisessa on lämmintä ja toisessa kylmää ilmaa. Pallot poukkoilisivat eri nopeuksilla sen mukaan, kummassa onkalossa käsi on. Saa hyödyntää vapaasti, ideoilla ei ole patenttisuojaa.

Mietiskelin myös sitä, kuinka vahingollista simulaatioihin liittyvät "virheet" ovat. Saako niistä fysiikan sieluunsa vahingon? Pingispallot keveydestään huolimatta ovat paljon enemmän painovoimapaholaisen vankeja kuin oikeat kaasuatomit tai molekyylit. Ne kasautuvat simulaatiossa selvästi ison laatikon alaosaan, kun reaalikaasut täyttävät suljetun tilan tasaisesti. Yleispätevää vastausta tuskin on, mutta yleisesti ottaen olen sitä mieltä, että hieman väärät mielikuvat voidaan hyväksyä, jos vastapainona on kohteesta saatu havainnollisuus. "Väärin sammutettu" ja "väärin opetettu" ovat lauseita, jotka kuuluvat samaan happamien pihlajanmarjojen hilloon. Minusta vähän väärin opetettu on paljon parempi kuin virheiden pelossa kokonaan opettamatta jättäminen. Pätee myös sammuttamiseen.

Toinen kiehtova "analoginen" lisäketodellisuuslaite tiedekeskuksessa oli vanha kunnon Foucaultin heiluri. Se oli täällä mielestäni parempi kuin Heurekassa, jossa heiluri toimii vain painovoiman liikuttamana ja siitä syystä sen heilahtelu ei voi kestää kovin kauaa. Täällä kuten monessa muussakin paikassa heilurin heilahtelua on avitettu moottorilla. Silloin katsoja kykenee näkemään miten heilurin heilahdustaso kiertyy pitkän ajan kuluessa.  Yksi hieno piirre Foucaultin heilurissa on se, että sen ääreen on pysähdyttävä. Lisäketodellista havaintoa maapallon pyörimisestä ei voi saada kerran katsomalla eikä pikakelauksella.

Copernicuksen, kuten monen muunkin tiedekeskuksen keskiössä on Foucaultin heiluri. Se vie paljon tilaa, mutta on näyttävä ja yleensä aika toimintavarmakin - ainakin niin kauan kuin maapallo jaksaa pyöriä. 

Heilurin heilahdustason kiertymisen heilahtelun alusta lähtien näkee selvästi kaatuneiden keppien määrästä.

Analogia tämän kuvan kanssa on niin herkullinen, että en malttanut olla laittamatta sitä. Tapahtumapaikka on edelleen Varsova ja kyseessä on Puolan kommunismista irtaantumisessa keskeisestä pyöreän pöydän neuvottelusta vuonna 1989. Pääosassa yllä jo mainittu Lech Walesa.

Tällaisissa pitkään venyvissä kokouksissa voisi olla hyvä kirittäjä laittaa kattoon Foucaultin heiluri, joka kopsahtaa kokousedustajan otsaan kohdalle tullessaan. Kokouksen keston voisi laskea pöydälle kupsahtaneinein päiden päämäärästä - olettaen tietysti, että paikan leveyspiiri tunnetaan.

Foucaultin heiluri täyttää minusta lisäketodellisuuslaitteen keskeisen ominaisuuden. Se tuo näkymättömän näkyväksi. Tässä tapauksessa näkymätön tai pikemminkin kokematon asia maapallon pyöriminen, jonka johdosta ja todisteena Foucaultin heiluri kiertyy maapallon pyörimisnopeuden ja paikan leveyspiirin määräämällä nopeudella. Viimeksi mainitussa suhteessa olemme näillä korkeilla leveysasteilla "paremmassa" asemassa kuin etelässä. Kiertyminenhän on sitä suurempaa, mitä kauempana päiväntasaajasta ollaan.

ps. Lähtiessäni kotiin sain Puolan lentoyhtiöltä LOT:lta viestin kännykkääni. Barack Obama tulee kaupunkiin iltapäivällä ja kaikki tiet lentokentälle saattavat olla suljettuja. Olisi syytä lähteä jo aamupäivällä lentokentälle, vaikka lähtöni olikin  vasta klo 19.

Minä herkkäuskoisena ja viranomaistiedotteita noudattavana kansalaisena tein niin. Turhaan. Tiet eivät olleet suljettuja ja  Obama saapui vasta klo 19:30. Sen sijaan mikään taho ei varoittanut minun Suomen päässä olleesta laukunheittäjien pistelakosta, joka takia koneeni lähti neljä tuntia myöhässä. Näin ollen disinformaation ja missinformaation takia vietin lentokentällä 12 tuntia, pääosin puolalaiseen lisäketodellisuuteen syvemmin tutustuen.

Tätä lähemmäksi en ole Amerikan presidenttiä koskaan päässyt ja tuskin tulen pääsemäänkään. Air Force One juuri Varsovan lentokentälle laskeutuneena.

Puolalaisessa saunassa

 

Tämä sauna ei ollut muuta suomalaista nähnytkään kuin kuvan ottajan ja hänen Nokiansa, jolla kuva otettiin. Puolalainen saunojan self made survival kit. Roskapönttö ja vessaharjan alusastia.

Kävin viime kesänä Puolassa tiedekeskuskonferenssissa. Hotellini oli kaupungin laidalla. Sen respassa oli mainita, että hotellissa on suomalainen sauna. Pakkohan sitä oli kokeilla. Hintakin oli varsin kohtuullinen, noin 5 euroa + 3 euroa per henkilö. Yksin kun olin liikkeellä, niin 8 euron sijoitus hygieniaan ei tuntunut liian suurelta.  Kun kysyin, että milloin sauna olisi vapaa, niin sen luvattiin olevan käytettävissäni 2 tunnin päästä.

Hotellin ovipoika päästi minut saunaan. Kun kyselin pukuhuonetta, niin poika osoitti minulle suihkun vieressä pesuhuoneessa olevaa kahta vaatenaulaa. Niihin saisi ripustaa vaatteet. Pukuhuoneen puutteen sitten korvasi kaksi todella isoa wc:tä, miehille ja naisille tietysti omat. Toiletit pesutiloineen olivat isommat kuin saunan pesu- ja löylyhuoneet yhteensä. En ollut oikein varma, tultiinko tänne ensisijaisesti tekemään tarpeet ja vasta toissijaisesti saunomaan?

 Yhdistetty puku- ja suihkuhuone. Epämääräinen musta möykky kuvan keskellä on kirjoittajan vaatteet.

Löylyhuoneessa saunan pitkän lämmitysajan salaisuus selvisi minulle. Sauna oli tulikuuma, mittari näytti 130 astetta. Lauteilla istuminen olisi vaatinut ainakin takapuolesta eristetyt housut. Löylyn heittäminen olisi ollut  varma itsemurhalta. Tosin nähtävästi ei ollut tarkoituskaan, että löylyä heitettäisiin, sillä minkäänlaisia löylyastioita ei ollut koko saunassa.

Alastonna muttei neuvotonna. Otin vessan roskakorin löylyvesiasiaksi ja vessaharjan astian kiipoksi (pesin sen aika huolella ensin). Kylmää vettä ensin reilusti seinille ja lauteille. Sen jälkeen saunominen, jopa löylyn heitto oli mahdollista. Mikä lämmityksessä tuhlattiin, se kiuaskivien määrässä säästettiin. Niitä oli korkeintaan 10 kiloa, vastukset loistivat punaisina niiden harvoista väleistä.

Lauteilla pohdiskelin, kuinka hieno fysikaalinen ja fysiologinen lämpöopin oppimiskohde sauna voisi olla. Tässä opin saunassa kylpijällä olisi tietysti päässä viimeisin pedagogistekninen vempain:   lisäketodellisuuskypärä , joka paitsi suojaisi korvia palamiselta myös antaisi tarpeellista dataa ja tietoa saunomisen edistyessä. Lämpötilan, kosteusprosentin, kehotuksen lähteä pois ennen kuin henki lähtee. Samaista laitetta voisivat käyttää myös saunomisen mm. kilpailuihin valmentautuvat kilpailijat - sikäli kun kisoja enää järjestetään Heinolan traagisten tapahtumien jälkeen. Kaimapoika Sauna-Timokin olisi varmaan paremmassa hapessa, jos olisi valmistautunut kisaan vähän tieteellisemmin.  Lauteille tuupertuneesta Vladimir Ladyženskista nyt puhumattakaan.

Puolalaisella saunan suunnittelijalla olisi voinut olla oma lisäketodellisuuskypäränsä piirustuspöydän ääressä. Tosin saman tiedon olisi saanut helpommin käymällä ennen "suomalaisen" saunan rakentamista oikeassa suomalaisessa saunassa.

Kun vein avaimen takaisin respaan, niin minulta tiedusteltiin, miltä suomalainen sauna tuntui suomalaisesta. Valehtelin sujuvasti olleeni hieman pettynyt vain yhteen asiaan.

- Ja mikähän se mahtoi olla? Ei tarpeeksi kuumaa?

- Kiuas oli ruotsalainen Tylö!  

Temppu ja kuinka se tehdään

Heurekan innoittajien tempuista näyttävimpiä on narun päässä olevan kahvikupin pudottaminen siten, että sormen ympärille kiertyvä naru pysäyttää kupin ennen kuin se ehtii pudota maahan. Jos ja kun katsojat ryhtyvät kyselemään tempun takana olevaa fysiikkaa, niin sen kerrotaan olevan aika monimutkaista. Ainakaan minun korviini ei ole tullut edes yhtään yritystä selittää, miten systeemi käyttäytyy fysikaalisesti.

Minäpä yritän. Kuvassa on keskeisimmät sekä mukiin että narun toisessa päässä olevaan pieneen painoon vaikuttavat voimat. Suureet ja niiden arvot (minun kotona tekemässäni kokeessa) ovat seuraavat:

M = mukin massa = 0,266 kg

m = painon massa = 0,032 kg

g = maan vetovoiman kiihtyvyys = 9,83 m/s²

a = mukin putoamiskiihtyvyys ja painon keskeiskiihtyvyys (alussa lähes g, putoaa nopeasti nollaan)

µ = langan ja sormen välinen kitkakerroin (tuntematon)

N = langan sormeen kohdistama normaalivoima (ei vakio)

r  = ympyräliikkeessä olevan painon pyörimissäde (ei vakio)

v = ympyräliikkeessä olevan painon ratanopeus (ei vakio)

Muki pyrkii alaspäin painollaan eli voimalla Mg = 0,266 kg * 9,83m/s^2= 2,6 N

Tätä liikettä vastustaa kolme eri tekijää

1. Narun ja sormen välinen kitka µN

2. Kun naru vetää painoa voimalla ma, niin Newtonin III lain mukaan paino aiheuttaa naruun saman suuruisen, mutta vastakkaisen voiman.

3. Paino on pyörimisliikkeessä, tosin radalla, jonka säde pienenee niin kauan kuin paino putoaa alaspäin. Naru pitää sen radalla voimalla mv^2/r, jolloin edelleen Newtonin III:n mukaan naruun kohdistuu saman suuntainen mutta vastakkainen voima.

On varsin ilmeistä, että putoavan mukin pysähtyminen vaatii seuraavan epäyhtälön voimassa olemisen.

Siihen helppous sitten loppuukin. Epähtälön oikean puolen suureet v, r, N ja a nimittäin riippuvat paitsi mukin painosta Mg myös toinen toisistaan. Mitkä ovat niiden keskinäiset riippuvuudet? Epähtälön ratkaiseminen suljetussa muodossa on jos ei  mahdotonta niin ainakin vaikeaa (siis minä en osaa).

Jos teoriaherrana olo ei onnistu, niin yritetään käytännön kautta. Tein putoavasta kupista pienen videon. Videon hidastetussa osassa voidaan havaita, missä kohtaa pyörähtävä narun osa on, kun kuppi jää paikoilleen.

Videosta otettu kaksi ruutua, joiden välinen aika on 1/30 sekuntia. Kuvat on laitettu päällekkäin, jolloin narun kiertymä saadaan selville. Naruja on korostettu punaisella värillä.

Kupin pysähtyessä pyörivä naru on noin kello 8:n kohdalla. 1/30 sekunnin kulutta se on kiertynyt 22 astetta enemmän. Narun pituus on yhteensä tasan 1 metri, joten mittaamalla vaikka kuvasta pyörivän narun pituudeksi tällä hetkellä saadaan 42 cm. Näistä arvoista voidaan laskea riittävän tarkasti painon nopeus kupin pysähtyessä.

Keskeisvoima on siis

Ylöspäin suuntautuvan voiman täytyy olla suurempi kuin kupin painon, jotta putoamassa oleva kuppi pysähtyisi. jarruttava voima kasvaa kuitenkin niin nopeasti narun kierryttyä yli yhden kierroksen sormen ympärille, että pysähtyy nopeasti ja voidaan hyvin approksimoida kupin pysähtyessä voimien olevan yhtä suuret. Tästä lisähidastetusta videosta voi tutkia asiaa. 

Mitä tästä voidaan päätellä? Ei vielä hirveän paljon. Kupin putoamisen pysähtyessä siihen vaikuttavasta 2,6 N ylöspäin suuntautuvasta voimasta noin 70% johtuu narun pyörimisestä ja 30% kitkasta. Keskeiskiihtyvyys lisää narun jännitystä ja painaa sitä tiukemmin sormen ympärille. Se lisää kitkaan vaikuttavaa normaalivoimaa N. Siksi on vaikeaa päätellä, kuinka iso osuus jarruttavasta voimasta on kitkalla ja kuinka iso ympyräliikkeestä johtuvasta langan jännityksellä.  Toisessa päässä olevan painon massan hitaudesta aiheutuva  jarrutus mukiin on niin vähäistä, että se voidaan jättää huomiotta.

Yritetty siis on, mutta aika laihoin tuloksin. Matemaattisen mallin tilanteesta sain aikaisekseni, mutta sen ratkaiseminen, eli laskea yhtälöstä vaikka se, kuinka paljon kuppi putoaa, jäi minulta tekemättä. Tässä haastetta fysikaalis-matemaattisesti suuntautuneille poikkitieteilijöille. Omia laskelmia varten lienee syytä selvittää vielä ainakin narun ja sormen välisen kitkakertoimen arvo ja sormen paksuus. Sormi ei ole fysikaalisessa mielessä kiinteä kappale, vaan enempi vähempi joustavaa materiaalia. Siksi narun ja sormen välinen kitkakerroinkaan ei ole vakio, vaan riippuu myös siitä, kuinka tiukkaan naru on kiertyneenä sormen ympärille.

Joten laskennallisia haasteita riittää - jos aikoo selittää putoavan, mutta pysähtyvän kahvikupin fysiikkaa vähän eksaktimmalla kuin sillä perinteisellä tavalla: "Se on aika monimutkaista". Kuten sanottua, minulta se ei onnistunut tämän paremmin eikä lähestulkoonkaan näinkään syvällistä esitystä asiasta voi olla demoa yleisölle näytettäessä. Tuskin kuitenkaan on "temppua" yleisölle näyttävälle haitaksi, jos hänellä on hieman "sisäpiirin tietoa" siitä, millaista fysiikkaa se pitää sisällään.

Jälkikirjoitus

Sain henkilökohtaiseen postiini aika kiukkuista palautetta siitä, että olen tällä kirjoituksellani jotenkin aliarvostanut innoittajien työtä. Kun tämä ei ole ollut vähäisimmässä määrin tarkoitukseni, niin muutama sananen puolustukseksi.

1. Arvostan suuresti innoittajien työtä Heurekan toiminnan yhtenä keskeisenä kulmakivenä. Vaikka törppö olenkin monessa mielessä, niin törppö en ole, että lähtisin heitä syyttä suotta moittimaan julkisesti.

2. On selvää, että erilaisten "temppujen" fysiikkaan ei voida paneutua niiden yhteydessä. Se ei ole missään mielessä mielekästä. Fyysikkona kiinnostuin tästä esityksestä, kun kuulin Nean sanovan sen takana olevan fysiikan olevan vaikeaa. Päätin tutkia kuinka vaikeaa. Olihan se, minulta loppuivat eväät ongelman fysikaalisen ratkaisun suhteen. Laitoin tiedon blogistani eteenpäin siitä syystä, että tätä "temppua" näyttävät innoittajat ja muut siitä ehkä kiinnostuneet voisivat halutessaan kurkistaa sen takana olevan fysiikkaan. Ja ennen kaikkea siihen, että fyysikkokin joutuu nostamaan kädet pystyyn ratkaisua etsiessään.

3. Videon MAOL:n syyspäiviltä laitoin nimenomaan siksi, että siitä käy hyvin ilmi, kuinka hienosti Nea vetää opettajat mukaansa tämän "tempun" avulla. Kerta kaikkiaan nappisuoritus. Jos joku kokee tämän kunnianosoituksen innoittajien hienolle työlle pilkaksi heitä kohtaan, niin pyydän syvästi anteeksi. Se ei ole ollut tarkoitukseni. Erityisesti minulla ei ole mitään kompetenssia eikä halua tulla mestaroimaan, miten innoittajien pitäisi hoitaa postinsa. Poikkitieteellistä fysikaalista taustatietoa on tarkoitus antaa tällä palstalla, ei toisten työn halveksintaa.

 Tämä kuvapari kertonee paljon tilanteesta. Olin yhdessä Heureka-opettajan Nea Törnwallin kanssa Keravalla MAOL ry:n syyspäivillä esittelemässä Heurekan oppimiskeskuksen tarjontaa. Minä lähinnä kertomassa rakentamastani oppimispolusta. 

Kun vierekkäin laitetaan sujuvasti kahdella kotimaisella kielellä elävää demoa esittelevä viehättävä nuori naisihminen ja tietokoneruudulta omaa sanomaansa pelkällä suomellakin vähän takeltaen esittelevä elähtänyt vaari, niin ei ole vaikeaa arvata, kumman luona käy kuhinaa. Pyysin Heurekan oppimiskeskuksen johtajaa Matti Rossia ottamaan kuvan, kun minunkin luonani olisi "vähän enemmän ihmisiä". Parhaansa Matti varmaan teki, mutta tulos yllä.

Lisää aiheesta

Lauantaina 8.10.2011 Iltalehti siteerasi toista aviisia, elikkä Tähdet ja avaruus –lehteä. Seuraavalla otsikolla ja pienellä jutulla.

Luvassa on kirkkaita tähdenlentoja, kertoo Tähdet ja avaruus -lehti.

Lauantai-illalle odotetaan draconidien tähdenlentoparven purkausta, kertoo Tähdet ja avaruus -lehti verkkosivuillaan. Normaalisti draconidit on vaatimaton parvi, mutta tänä vuonna osa tutkijoista ennustaa sen yltävän purkaukseen.

Draconidien mahdollinen purkaus osuu parhaiten nähtäväksi Suomessa. Tästä syystä kansainvälinen draconidi-havaintokampanja toteutetaan pääosin Suomen ilmatilassa.

Suomen ylle lentää lauantai-iltana kaksi yhdysvaltalaisten ja eurooppalaisten tutkijoiden havaintolentokonetta.

Parven maksimin odotetaan osuvan lauantaille noin kello kymmenen ja puoli yhdentoista välille. Alkuillasta voi myös näkyä joitakin yksittäisiä hyvin kirkkaita tähdenlentoja.

Kävin illalla kurkkimassa taivaalle, mutta Rekolan horisontissa taivas oli sen verran pilvien peitossa, että mitään ei näkynyt. Jotkut saivat hienoja kuvia. Enemmän kuin näkemättömät tähdenlennot minua jäi askarruttamaan Iltalehden aiheesta syvempää tietoa antavat linkit. Niitä oli lehden omille sivuille viitaten kolme kappaletta.

Lisää aiheesta:

Tutkimus: Suomi on sisäsiittoinen 28.10.2009 13:42

Storbacka juoksi 800 metrin kärkiajan 16.08.2009 17:24

Stubb vierailee USA:ssa toukokuussa 01.04.2009 11:31

Jutut lyhykäisyydessään alla

Suomi on sisäsiittoinen

Tuore tutkimus tituleeraa Suomea sisäänpäin kääntyneeksi maailman peräkyläksi. Tutkimuksen mukaan Suomi on huomattavasti vähemmän kansainvälistynyt kuin mitä usein ajatellaan.

Asiasta uutisoi Alma Median Helsingin toimitus.

18 asiantuntijaa ympäri maailmaa arvioi Suomen kansainvälisyyttä tuoreessa selvityksessä.

Asiantuntijoiden mukaan sisäsiittoinen Suomi pelottaa ulkomaalaista työvoimaa. Tutkijat ja yritykset karttavat Suomea, eivätkä tuo maahamme kaivattua globaalia osaamista.

Ulkomaalaisen osaamisen määrä on vähentynyt Suomessa. Samalla suomalaisen työvoiman liikkuvuus ulkomaille on hyytynyt.

Storbacka juoksi 800 metrin kärkiajan

Karin Storbacka juoksi naisten 800 metrin kotimaiseksi kärkiajaksi 2.02,99 lauantaina Cardiffissa. IK Falkenia edustava Storbacka pinni samalla uuden matkaennätyksensä.

Cardiffin kansainvälisten kisojen 800 metriä voitti Britannian Claire Gibson ajalla 2.01,34. Storbacka sijoittui viidenneksi.

Stubb vierailee USA:ssa toukokuussa

Ulkoministeri Alexander Stubb (kok) tapaa tänä keväänä amerikkalaisen kollegansa Hillary Clintonin Yhdysvalloissa. Vierailu on toukokuun alkupuolella.

Stubb ja Yhdysvaltain tuore ulkoministeri Clinton ovat jo tavanneet kansainvälisten kokousten yhteydessä. Stubb kertoi tapaamisesta kirjansa julkistamistilaisuuden yhteydessä Helsingissä. Tarkkaa vierailupäivää ei vielä sanottu.

Sisäsiittoisuusartikkelin yhteyden tähdenlentoihin ymmärrän vielä jotenkin sokean logiikan tasolla, puhutaanhan molemmissa artikkelissa tutkijoista. Mutta miten Karin Storbackan 800 kärkiaika ja Alexander Stubbin USA:n vierailu liittyvät millään tapaa siihen, siitä voisi joku fiksumpi valistaa minua. Muuten menee turhan poikkitieteelliseksi jopa tässä kontekstissa.

Olisiko kuitenkin niin, että ihmisen aivojen kontrollissa olevat linkitykset toimivat vielä toistaiseksi paremmin kuin automaattinen ilman älyä toimiva linkitysrobotti?

Paljastaako valokuva salarakkaan?

 

Wikipedia tietää:

"Punastuminen on tila, jossa ihmisen kasvoihin, kaulaan ja ylävartalolle ilmestyy läiskittäistä punoitusta pintaverisuonten laajentuessa ja pintaverenkierron lisääntyessä. Punastumisreaktion synnyttää autonominen eli tahdosta riippumaton sympaattinen hermojärjestelmä.

Punastuminen on hyvin yksilöllistä. Joillakin ihmisillä punastuminen on yleistä sosiaalisissa tilanteissa, mutta toisilla sitä ilmenee vain hyvin harvoin. Punastumisen aiheuttaa yleensä jännitys, joka voi liittyä nolostumiseen, epävarmuuteen tai valehteluun, myös positiivisiin tunteisiin kuten vaikka ihastumiseen. Voimakas kiukku tai viha voivat myös aiheuttaa punastumista. Punastumiseen liittyy usein samanaikainen voimakas hikoilun tunne.

Vaikka punastumisen mekanismi tunnetaan hyvin, sen perimmäistä tarkoitusta ei ole toistaiseksi kyetty kovin hyvin selvittämään. On kuitenkin arveltu, että ihmisen varhaisten edeltäjien keskuudessa punastuminen on saattanut olla tärkeä signaali. Ennen puheen perustuvan viestinnän kehittymistä kasvojen värin vaihtumisella saattoi olla ilmeiden ja eleiden ohella huomattava merkitys yksilön todellisen mielentilan välittämisessä muille lajikumppaneille."

Valtiovarainministeri Jutta Urpilainen oli 5.10.2011 MTV3:n Huomenta Suomi -ohjelman vieraana. Haastattelun kuluessa Jutan avonainen rintamus alkoi punottaa sitä enemmän, mitä pidemmälle ohjelma eteni. Syytä on mahdotonta tietää, mutta jos minulta kysyttäisiin, niin veikkaisin salaista ihastumista jyhkeään toimittaja Lauri Karhuvaaraan.

Hyviä uutisia Kreikasta, osa II

 Kuva: Kari Pekonen

Sain tänään Jutalta sähköpostia valtionvarainministeriöstä. Sen luettuani olenkin selvillä siitä, mistä tästä vakuusjärjestelyssä oikein on kysymys. Kyllähän monimutkaisetkin asia selkenevät, kun vain selitetään. Toivottavaa olisi, että Jutta itsekin ymmärtäisi. Siitä kun en ole aivan varma.

"Ohessa on käyttöösi valtiovarainministeriössä laadittuja kysymyksiä ja vastauksia, jotka selventävät Kreikan lainaohjelman vakuusjärjestelyä.

Kysymyksiä ja vastauksia Kreikan lainaohjelman vakuusjärjestelystä

* Mistä 3.10 euroryhmän kokouksessa sovittiin?
Kokouksessa sovittiin periaatteista ja ehdoista, joilla vakuuksia voidaan saada ja vakuuksien määräytymisperusteista. Arvioitu vakuussumma on 880 milj. euroa. Sitä täsmen­netään kun Kreikan uuden lainaohjelman lopullisista yksityiskohdista ja määrästä sovitaan. Siihen vaikuttaa myös IMF:n osuus uudesta laina­ohjelmasta.


* Mitä vakuudet käytännössä ovat?
Varsinaiset vakuudet ovat AAA-luottoluokituksen arvopapereita. Näiden hankkiminen toteutetaan vaiheittain myymällä investointipankin välityksellä Kreikan valtion velkakirjoja. Kreikan valtio lainaa kreikkalaisille pankeille Kreikan valtion velkakirjoja. Kreikkalaiset pankit vaihtavat velkakirjat maan keskuspankissa oleviin velkakirjoihin, jotka ovat siellä keskuspankkioperaatioiden vakuutena. Kyseiset pankit luovut­tavat riittävän määrän kyseisiä velkakirjoja kolmantena tahona toimivalle asiamiehelle (Trustee), joka on käytännössä kansainvälinen investointipankki. Asiamies myy ao. velkakirjat markkina­hintaan ja niistä saatavat tulot talletetaan erillistilille ja sijoitetaan edelleen turvallisiin velkakirjoihin. Suomelle ei aiheudu tästä riskiä.

Saavutettu neuvottelutulos pitää sisällään paljon samoja elementtejä kuin Kreikan ja Suomen elokuussa neuvottelema käteisvakuusmalli.

* Kuinka mekanismi toimii käytännössä?
Erillistilillä olevat arvopaperit toimivat vakuutena sitä tilannetta silmällä pitäen, jossa Kreikka on jättänyt maksamatta ERVV:ltä saamansa lainat ja niitä koskeva, Suomen antama takaus laukeaa maksettavaksi ERVV:lle. Jos taas Kreikan valtio hoitaa ERVV-lainansa takaisinmaksun sovitun mukaisesti, palautuu vakuus ja sille kertynyt korko Kreikan pankeille, jotka palauttavat sen edelleen Kreikan valtiolle.

Kreikan valtion velkakirjojen likviditeetti on nykyisin heikko, minkä johdosta ei ole perus­teltua pyrkiä niiden myymiseen markkinoilla yhdellä kertaa. Em. operaatio toteutetaan vaiheissa siten, että asiamies myy velkakirjat erissä vuosien 2011–2014 kuluessa, sitä mukaa kun Kreikan uusi lainaohjelma tullaan maksamaan ja Suomelle kertyy vastuuta.

* Miksi järjestely on näin monimutkainen?
Osaan Kreikan valtion velkakirjoista sisältyy ns. panttaamattomuussitoumuslauseke (negative pledge), jonka mukaan kyseisen velkakirjan haltijan asemaa ei saa heikentää suhteessa muihin velkojiin, tai velka erääntyy välittömästi Kreikan valtion maksettavaksi. Tällaisen tilanteen syntyminen on estettävä. Kreikkalaisten pankkien kautta toteutettuna vakuusjärjestely ei muuta muiden velkojien suhteellista asemaa.

* Kuinka suuri vakuus saadaan?
Suomen saaman vakuuden suuruus tulee olemaan noin 880 milj. euroa. Lähtökohta­oletuksena on, että Suomen osuus uudesta lainaohjelmasta tulee olemaan noin 2,2 mrd. euroa. Vakuuden määrä perustuu luottoluokituslaitosten käyttämään arvioon velkakirjan­haltijoille aiheutuvasta tappiosta maksukyvyttömyystapauksessa (joka on 40 % velka­pääomasta) sekä korkoon. Mikäli alkupääoma on 880 milj. euroa, kasvaisi se esimerkiksi runsaalla 3 prosentin vuosikorolla 30 vuodessa jo 2,2 mrd. euroon, mikä vastaa Suomen nimellistä lainaosuutta uudessa Kreikka-ohjelmassa.

On syytä huomioida, että 21.7. päämieskokouksessa sovitun mukaisesti Kreikka ei voisi aiheuttaa ERVV:lle tappioita kymmenen ensimmäisen lainavuoden aikana, koska Kreikan ei tarvitse lyhentää lainaa tai maksaa korkoa tänä aikana.

* Miksi hypoteettiseksi tappioksi arvioidaan Kreikan osalta 40% velasta?
Tämä on luottoluokituslaitos Standard & Poor’sin yleisesti käyttämä oletus, joka perustuu historialliseen tilastoaineistoon maksukyvyttömyystilanteissa. Esimerkiksi: Jos Suomen lainaosuus olisi 2,2 mrd. euroa, 40 %:n tappio vastaisi 880 miljoonan euron suuruisen takauksen laukeamista maksettavaksi.

* Miten julkisuudessa mainittu 20 %:in vakuus takauksesta liittyy ratkaisuun?
Vakuuden suuruus suhteessa lainaosuuteen on Suomen riskienhallinnan kannalta keskeisin kysymys. Vakuuden alkusijoitus on 40 % Suomen laskennallisesta laina­osuudesta. Oletetun n. 3 % koron tasolla sijoitus vastaa 30 vuoden kuluttua Suomen laskettua lainaosuutta (noin 2,2 mrd. euroa). Kun kyseiseen laskennalliseen lainaosuuteen lisätään mahdollinen EKP:n väliaikainen vakuus ja tälle summalle lasketaan 165 %:n ylitakaus, joka tarvitaan ERVV:n AAA-luokitukseen, on vakuuden alkusijoitus karkeasti 20 % laskennallisesta takaus­summasta.
Vakuuden arvon liittäminen Suomen osuuteen lainapääomasta (koko takauksen sijaan) on perusteltua sen johdosta, että ylitakaus ei liity Kreikan mahdollisiin maksuvaikeuksiin, vaan muiden takaajien mahdollisiin ongelmiin. Ylitakaus laukeaa maksettavaksi vain siinä tapauksessa, että joku tai jotkin muut takaajina toimivista euromaista eivät pystyisikään vastaamaan omasta takausosuudestaan. Mikäli näin kävisi, syntyisi siitä velkasuhde yli­takauksen maksaneiden maiden ja takauksensa pettäneiden maiden välille, ts. Suomi perisi tällöin saataviaan kyseisiltä mailta tarvittaessa hyvinkin pitkän ajanjakson kuluessa.

* Mitä ehtoja vakuuksien saamiseen liittyy?
Vakuuksia saava valtio: 1) luopuu ERVV:n mahdollisesti voitto-osuudestaan; 2) vakuus maksetaan paljon takauksen laukeamista myöhemmin (15-30 v., ml. korot); ja 3) Suomi maksaa EVM:n pääoman (1.44 mrd. euroa) kerralla.

* Miksi Suomi voi hyväksyä ehdot?
Suomen alhaisten velan­hoitokustannuksien johdosta esimerkiksi EVM:n pääoman maksaminen kerralla ei ole Suomelle merkittävä ongelma, toisin kuin mitä se olisi niille jäsenmaille, joiden velanhoitokustannukset ylittävät selvästi EVM:n pääomasta saatavan korkotuoton. ERVV:n menetettyyn voitto-osuuden arvioidaan jäävän nykyisillä korko-oletuksilla vaatimattomaksi suhteessa vakuusjärjestelystä saatavaan hyötyyn.
Kaikki euromaat arvioivat kokonaisuutta omista lähtökohdistaan. Suomelle vakuusmallin ehdot ovat edulliset.

* Maksavatko vakuudet jotain?
Jos luottoluokitus on alle AAA tai valtion velkatason on korkea, vakuusjärjestely ei ole mielekäs, koska tällöin EVM:n pääoman kertasuosituksesta aiheutuisi näille maille kustannuksia.

* Miksi Suomi voi maksaa kerralla EVM:n pääomaosuutensa kerralla?
EVM:n maksamisella kerralla ei aiheudu nettomääräistä haittaa Suomelle AAA-luottoluokituksen vuoksi. EVM:n maksetun pääoman suuruus on Suomelle n. 1,4 mrd. euroa. Suomi saa lainaa suunnilleen samalla korolla, kuin jonka EVM saa omille sijoituksilleen (AAA) pääoman tuottona. Muutoin Suomi maksaisi pääoman 2013 alkaen viidessä n. 280 milj. euron erässä vuoteen 2017 mennessä.

* Aiheutuisiko etupainotteisesta maksusta Suomelle haittaa tai riskiä?
Ei aiheudu. Jos EVM tarvitsisi lisäpääomaa (tilanteessa jossa Suomi on maksanut koko osuutensa ja muut eivät), muut maat joutuisivat maksamaan puuttuvat pääomaosuudet ensin.

* Miksi Suomi on valmis luopumaan ERVV:n voitoista?
Vakuusjärjestelyn toimeenpanoon liittyy ehto, jonka mukaan Suomen osuus mahdollisesta ERVV:nvoitoista liittyen Kreikan lainapakettiin alenee odotetun tappio-osuuden verran (arvio 40 %). Suomen näkemyksen mukaan ERVV:n ei tule tekemään voittoja merkittävässä määrin. Euroalueen pää­miesten 21.7. kokouksessa hyväksyttiin uusia linjauksia korkopolitiikkaan liittyen, minkä seurauksena tämä korkomarginaali ja siihen liittyvä voitto tulee tulevaisuudessa jäämään hyvin pieneksi. Tämä linjaus koskisi Kreikan uutta lainapakettia. Suomi ei myöskään ole hakemassa tukipaketista taloudellista hyötyä.

* Koskeeko vakuusjärjestely vain Suomea?
Vakuusjärjestely on avoin kaikille euromaille.

* Miksi muiden euromaiden ei oleteta hakevan vastaavia vakuuksia?
Vakuuksien saamiseen liittyvistä ehdoista etenkin EVM:n pääoman maksaminen kerralla on useimmille euromaille ongelmallinen kysymys, mistä kertoo se, että alkuperäisen EVM-ehdotuksen mukaista kolmen vuoden maksuaika pidennettiin neuvotteluiden tuloksena viiden vuoden mittaiseksi.

Niille jäsenmaille, joilla ei ole parasta AAA-luottoluokitusta aiheutuu ylimääräisiä korkomenoja EVM:n pääoman maksamisesta, koska heidän velanhoitokustannukset ylittävät EVM:n pääomalle saatavan korkotuoton. Toisaalta myös usealla AAA-maalla on budjet­ti­teknisiä syitä sille, miksi huomattavan suuren pääomaosuuden maksaminen kerralla olisi heille ongelmallista. Suomen tilanne poikkeaa tässä suhteessa muiden euromaiden tilanteesta, mikä on osaltaan vaikuttanut sovitun vakuusjärjestelyn sisältöön.

* Mikä on vakuuden kesto?
Vakuuden ajallinen kesto on Suomen kannalta tärkeä elementti. Eri tahot ovat esittäneet, että vakuudet olisivat voimassa vain osan laina-ajasta, ts. ne raukeaisivat esimerkiksi siinä vaiheessa, kun Kreikan voidaan todeta päässeen uskottavalle kasvu-uralle ja lainojen takaisinmaksu ei näytä enää uhanalaiselta. Tällaiset ratkaisut eivät ole Suomen hyväksyttävissä, minkä johdosta on päädytty ratkaisuun, jossa Suomen antaman takauksen lauetessa maksettavaksi, saa Suomi vakuuden vasta Kreikan ERVV-lainojen erääntyessä maksettavaksi. Suomi saa kuitenkin korkoa vakuudelleen takauksen laukeamis­ajankohdasta lähtien, millä voidaan kattaa tähän liittyvät Suomen velan­hoitokustannukset.

* Miksi Kreikan ja Suomen kesällä tekemää sopimusta ei voitu hyväksyä?
Suomi ja Kreikka tekivät yhteisesti euromaiden kanssa sovitulla tavalla elokuussa 2011 esityksen nk. käteisvakuusmallista. Käteismalli oli avaus keskustelulle ja pohdinnoille. Tällöin painotettiin sitä, että mallin on oltava kaikkien euromaiden hyväksyttävissä. Erityisesti IMF ja komissio pitivät tärkeänä, että vakuusmalli ei saisi johtaa Kreikan uuden lainaohjelman koon kasvattamiseen."